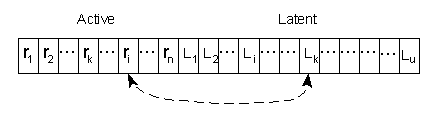Home › Research › The evolutionary model of industrial dynamics

The evolutionary model of industrial dynamics

The model stems from two streams of my research, namely:

  • Computer simulation of evolutionary processes (initiated in 1970s).
  • Joseph A. Schumpeter and evolutionary economics (since the end of 1980s).

For the first time, the model was published in 1992 (Kwasnicki and Kwasnicka, 1992). Since that time the model (with minor modifications) and its simulation results have been presented in different journals and books. The list of relevant publications is presented at the end of this note.

The model draws heavily from our earlier model of biological evolution, developed in the 1970s and 1980s by Halina Kwasnicka, Witold Kwasnicki and Roman Galar.

There is a close interrelationship between the model of industrial evolution and the general model of knowledge development presented in the first part of my book on Knowledge, Innovation and Economy.  Most ideas presented in the first part of this book are adjusted to the specific circumstances of industrial development and are expressed in the more formal, mathematical way.

General structure of the evolutionary industrial model

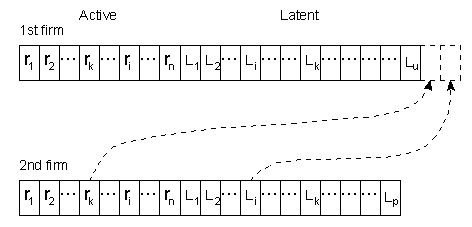
Basic mechanisms of generation of new sets of routines (inventions):

  • mutation (moderate modification) – autonomous research, in-house development
  • recombination, imitation
  • transition
  • transposition
  • recrudescence – search for radical novelty through reshaping of the active set of routines (large number of transpositions and/or frequent modifications by means of mutation)

transition

transposition

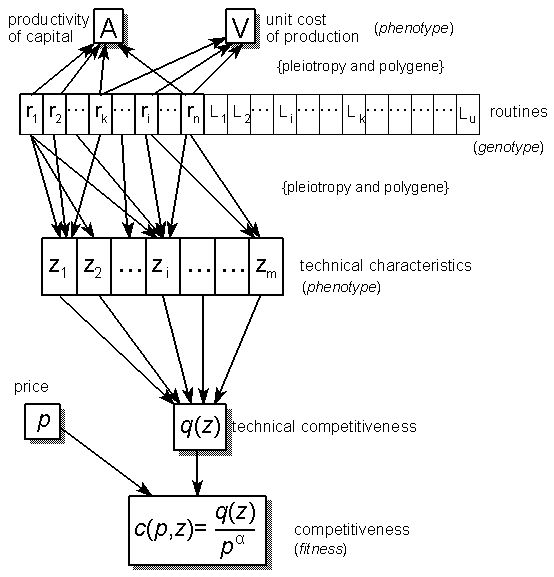
From routines to the competitiveness, productivity of capital and unit cost of production

 „Look! Here he comes, leaping across the mountains, bounding over the hills.” (Song of Solomon, 2:8)

Examples of industry evolution in the adaptive landscape, i.e., technical competitiveness q(z)
(two dimensions, each red star marks a single firm):

Source files of the software (written in Turbo Pascal 7.0).

Once I have been asked to state the main differences between my model and the well known Nelson and Winter model (presented, e.g. in their 1982 book on An Evolutionary Theory of Economic Change, Belknap Press, Cambridge, Mass. and London). Here is my short answer to that question.

The Nelson-Winter model and my model

In some way, it is an extension of the Nelson and Winter model (NW) presented in their 1982 book. The similarity of my model to the NW model is seen essentially in the general concept of evolutionary paradigm (selection and search for innovation processes), although there are essential differences, such as:

  • diversity of innovation types  – in the NW model firms can improve only capital productivity  (A). In my model, besides that type of innovation, firms can improve product performance (i.e., products’ technical characteristics, (z), technical competitiveness, q(z)), and also reduce the unit cost of production (V). Due to that diversity, it is possible to model such classical innovation types as embodied technical change (A) and disembodied technical change(V, q(z)), as well as product innovation V, q(z)) and process innovation (A, V, q(z)).
  • different price-setting procedures – the NW model set uniform price for all products of different firms via global demand function. In my model, each firm sets the price individually, considering such features as current production costs and current products’ characteristics and the existing market structure (the firms’ specific-price setting procedures cause a diversity of price at the industry level).
  • in my model, routines’ and products’ characteristics spaces (analogous to genotype and phenotype spaces in biology) cause different modes of innovation search. In the NW model, economic characteristics (namely, capital productivity) are modified directly. In my model, basic inventions and innovations stem from firms’ routines modifications and next through relevant transformations of routines values productivity of capital (A), unit costs of production (V), and products characteristics (z) are evaluated. I distinguish two types of routines, namely active and latent ones. Beside ‘classical’ search mechanism for innovation (invention) as mutation and recombination, I consider transition, transposition and recrudescence.
  • decision making procedure in the NW model has a form of a rather simple mathematical formula. In my model, the decision-making procedure includes such essential elements as investment constraints, the possibility of credit taking, the market’s current structure, diversified firms objectives, subjective evaluation of each firm concerning future behaviour of its competitors, etc.

The differences mentioned above make the model more realistic, but the natural consequence is that the model is more complex than the NW model.

I think that it is straightforward to generate numerous models (especially computer simulation ones) to describe different phenomena within a defined sphere of reality. Probably I represent a minority of researchers, but in my opinion, our general aim should be to develop a single, relatively general model of industrial dynamics allowing for description and explanation of different phenomena and also to enable identification of emerging properties of industrial development. Another important aim to build such a general model is to use it as an educational tool in economics courses of university curriculum (what I do presenting evolutionary economics in my university teaching). Therefore at the industry level (sometimes called mesoeconomics), I propose a general model which can be applied (through relevantly planned experiments) to describe phenomena observed in real industrial processes. Following this proposition, in the previous publications, I have used this model to describe important ‘stylised facts’, namely:

  • for a given market, the margin of price and firms’ profit increase with the concentration of industry (for example, from perfect competition, through oligopoly, duopoly, and ending with monopoly) (Kwasnicki, 1996, chapter 6);
  • there is a specific relationship between economies of scale and an industry concentration, namely the more significant the economies of scale the higher industry concentration (Kwasnicki, 1996, Ch. 6,Kwasnicki, 2000);
  • ‘the capital/labour ratio is rising more or less in proportion to productivity, and it is highest amongst the richest nations and lowest among the poorest, the capital/output ratio is much the same as between poor and rich countries? it is no higher in America … than it is in India’ (Kaldor, 1985, p. 67). Kaldor calls it ‘one of the best established ‘stylised facts’ of capitalist development (Kwasnicki, 1996, Ch. 7);
  • in the presence of innovation, there is no uniform price for all products sold on the market, but the great diversity of price is observed (Kwasnicki, 1996, Ch. 7, Kwasnicki, Kwasnicka, 1996a);
  • the emergence of innovation leads to temporal monopoly of the pioneer firm; at the first phase after innovation introduction, the monopoly firm gains extra profit that disappears over time, when competitors imitate the innovation (Kwasnicki, 1996, Ch. 7);
  • skewed distributions of business firms’ size and their long-term stability are the well  established ‘stylised facts’ of industrial demography; size distributions of firms of real industries are very similar (‘look like’) to Pareto, Yule, or log-normal distributions (conditions required for  the skewed distributions emergence are presented in Kwasnicki, 1998);
  • in multi-technological substitution processes of industrial development, the diffusion of a single technology has a form of the bell-shaped curve (which consists of four phases: an initial, introductory phase when the diffusion rate is not very high, followed by a stage of relatively quick diffusion; the third phase may be called the matured one in which the market share of the technology reaches maximum value; in the fourth phase, the market share of that technology declines, what is caused by the emergence of new, better technology). That pattern is  natural phenomena observed in simulations experiments. In (Kwasnicki, Kwasnicka, 1996) we have applied the simplified version of that model to forecasting diffusion-substitution processes;
  • industrial development is a unique historical process in which path-dependence and cumulative causation play an important role (Kwasnicki, 1996, Ch. 8). Path-dependency, increasing returns, a network effect (network externalities) are natural phenomena observed in the model’s behaviour (presented, e.g. Jena lecture);
  • cycles and fluctuations are a natural phenomenon found in industry development (Kwasnicki, Kwasnicka, 1994, Kwasnicki, 1996, chapters 6 and 7);
  • patterns of firms’ entry, exit, and industrial demography observed in the model are similar to records of industrial dynamics collected by David B. Audretsch, Steven Klepper and Kenneth L. Simons, Glenn R. Carrol and Michael T. Hannan, and many others (current work).
  • “On the basis of the presented results ,one may draw the conclusion that it is possible to imagine situations (industry regimes) in which highly concentrated industries behave like an industry with large number of firms being in a state of pure competition (namely, for small values of the cost ratio AV) and also industry regimes in which numerous competitors behave as oligopolist (or even as a monopolist), namely, for high values of the cost ratio AV. These findings are purely theoretical and ought to be verified using real data on industrial development.
  • The open question is if we observe such small and large values of the cost ratio in real industrial processes?
  • As a hypothesis, it may be stated that in real industrial processes, the cost factor is reduced in successive stages of an industry development because of introducing innovation reducing unit cost of production. Therefore, for matured innovative industries, we can expect higher competitive conditions of industrial evolution. (Kwasnicki, 2000)

Publications: